A. 参考文档

1、教程类

Queue + Stack：数据结构专辑仓库，有代码有实现，言简意赅；
The Queue data structure：系列文章，简短的介绍，但有具体的代码实现
Data Structures With JavaScript: Stack and Queue：来自 tutsplus 的详细教程文章
数据结构之栈和队列：总结了栈和队列的特点，罗列一些具体的应用；

2、应用类

数据结构(三)之栈结构：很详细的系列教程文章 - 栈，从认识结构到它的特点和应用场景，还附有面试题
数据结构(四)之队列结构：很详细的系列教程文章 - 队列，从认识结构到它的特点和应用场景，还附有面试题
栈与队列应用举例：用栈和队列模拟停车场管理
JavaScript数据结构与算法——栈及其应用：罗列了括号匹配、汉诺塔等具体应用，有图文解释
用栈解决迷宫问题（输出所有路径和最短路径）
数据结构与算法的JavaScript实现及应用 – 栈递归汉诺塔：介绍栈的基本操作和它的一些应用；在括号匹配检测，表达式求值，函数调用上的应用，本文还将给出表达式求值和汉诺塔的HTML5演示
Stack Data Structure：geeksforgeeks 中的 stack 专题

B. 正文

1、概述

队列的主要两个操作是 enqueue（入队）和 dequeue（出队）：

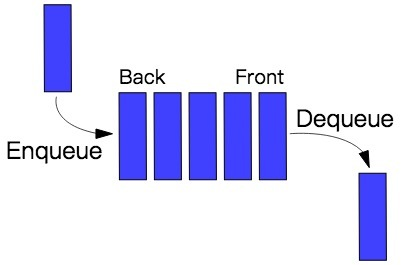
入队和出队

栈的主要两个操作是 push（入栈）和 pop（出栈）：

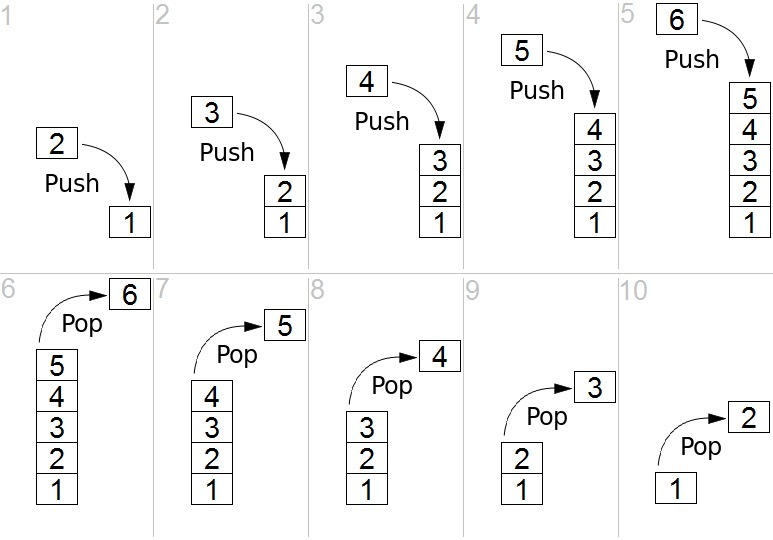
入栈和出栈

因为这两个库底层都是基于链表完成（重操作、轻查询），所以复杂度和链表是一样的。

队列比较常用的是广度优先遍历，在树中是层序遍历，在图中是无权图的最短路径；
栈能帮助你实现深度优先遍历等；

2、栈的应用

在 JS 中，队列和数组很相似，所以平时使用队列的场景会比较多；而对于栈这种数据结构接触的比较少，因此下面罗列的应用偏栈的应用比较多；

以下示例可以到 https://runkit.com/boycgit/ss-stack 查看具体的运行情况

2.1、十进制转二进制

来自文章数据结构(三)之栈结构

要把十进制转化成二进制，我们可以将该十进制数字和2整除（二进制是满二进一），直到结果是0为止。举个例子，把十进制的数字10转化成二进制的数字，过程大概是这样：

二进制

var Stack = require("ss-stack");
// 封装十进制转二进制的函数
function dec2bin(decNumer) {
    // 定义变量
    var stack = new Stack()
    var remainder;

    // 循环除法
    while (decNumer > 0) {
        remainder = decNumer % 2;
        decNumer = Math.floor(decNumer / 2);
        stack.push(remainder);
    }

    // 将数据取出
    var binayriStrng = ""
    while (!stack.isEmpty()) {
        binayriStrng += stack.pop();
    }
    return binayriStrng;
}

console.log(dec2bin(10));
console.log(dec2bin(233));
console.log(dec2bin(1000));

2.2、括号匹配问题

栈的应用——检测括号是否匹配：圆括号、方括号和大括号，其嵌套的顺序随意，使用栈这种数据结构能达到检测的目的；还有 JS括号匹配问题给出了两种解决方法；

示例来自 JS括号匹配问题

var Stack = require("ss-stack");
function validBraces(braces){
  let leftBraReg = /[\(\{\[]/, 
    // 栈
  rightBracket
  braces = braces.split('')
  let stack = new Stack();
  for(let bracket of braces) {
    if(leftBraReg.test(bracket)) {
      stack.push(bracket)
    }
    else {
      switch (bracket) {
          case ')':
          rightBracket = stack.pop()
          if(rightBracket !=='(') {
              return false
          }
          break
        case ']':
          rightBracket = stack.pop()
          if(rightBracket !=='[') {
              return false
          }
          break
        case '}':
          rightBracket = stack.pop()
          if(rightBracket !=='{') {
              return false
          }
          break
      }
    }
  }
  return stack.length === 0 ? true : false
}

validBraces("(){}[]")     // true 
validBraces("(}")      // false 
validBraces("[(])")    // false 
validBraces("([{}])")     // true

3、汉诺塔求解

用栈实现汉诺塔：由于汉诺塔的规则与栈的规则类似（先入后出），因此提出了用栈具体实现汉诺塔
Complexity for towers of Hanoi?：汉诺塔的复杂度是 O(2^n)

整个算法的思路是：

将 a 柱子上的 n-1 个盘子暂时移到 b 柱子上
a 柱子只剩下最大的盘子，把它移到目标柱子 c 上
最后再将 b 柱子上的 n-1 个盘子移到目标柱子 c 上

汉诺塔的递归法优雅而精妙，伪代码如下：

//将n个盘子按规则从a柱子，移动到c柱子
hanoi( n, a, b, c )
{
    if( n > 0 )
    {
        hanoi(n-1,a,c,b);
        //将a柱子的最上面的盘子移到c柱子
        c.push( a.pop() );
        hanoi(n-1,b,a,c);
    }
}

代码来自 JavaScript数据结构与算法——栈及其应用

var Stack = require("ss-stack");
var towerOfHanoi = function(n, from, help, to) {
  if (n > 0) {
    towerOfHanoi(n-1, from, to, help);
    to.push(from.pop());
    console.log('----------------');
    console.log(`from: ${from.stack.toArray()}`);
    console.log(`help: ${help.stack.toArray()}`);
    console.log(`to: ${to.stack.toArray()}`);
    towerOfHanoi(n-1, help, from, to);
  }
}

var a = new Stack(),
    b = new Stack(),
    c = new Stack(),
    n = 4;

for(let i = n; i > 0; i--) {
  a.push(i);
}
// test
towerOfHanoi(a.length, a, b, c);

4、调度场算法（中缀表达式转后缀表达式）

计算器的核心算法-JavaScript实现（逆波兰表达式）：很详细的教程，利用两个栈实现计算器，还有 demo；
javascript使用栈结构将中缀表达式转换为后缀表达式并计算值：例子详实，推荐
调度场算法系列：共 3 篇系列文章，循序渐进剖析调度场算法的来龙去脉，推荐

代码来自算法 - 调度场算法（Shunting Yard Algorithm）

/* ----------------------------------------------------
    调度场算法，将中缀转换过程后缀表达式
----------------------------------------------------- */
var Stack = require("ss-stack");

// 操作符优先级列表
var PRI_LEFT = 99;
var PRI_RIGHT = 100;
var PRI_TOKEN_MAP = {
    '+': 1,
    '-': 1,
    '*': 2,
    '/': 2,
    '(': PRI_LEFT,
    ')': PRI_RIGHT,
};

// 将中序转换成
function infixToPostfix(expression){
    expression = expression.replace(/\s*/g,""); // 去除所有空白字符
    var opStack = new Stack();
    var str = '';
    
    
    // 符号栈操作
    function calcToken(){
        str += opStack.pop();
    }
    
    for(let token of expression){
        var tokenPri = PRI_TOKEN_MAP[token] || 0;
        var peekTokenPri = opStack.peek && PRI_TOKEN_MAP[opStack.peek] || 0;   
        
        
        // console.log(opStack.stack.toArray());
        // 首先判断是否操作符
        if(tokenPri){
        
            // 情况 1： 栈顶不是左括号；入栈符号不是右括号
            // 循环判断当前栈顶符号，且优先级高于或等于将要入栈的元素，且栈顶不是左括号
            while(opStack.peek && PRI_TOKEN_MAP[opStack.peek] !== PRI_LEFT && tokenPri !== PRI_RIGHT && peekTokenPri >= tokenPri) {
                calcToken();
            }
            
            // 情况2：右括号准备入栈，
            if(tokenPri === PRI_RIGHT){
                // 将符号栈中元素依次弹出，则需要弹栈一直到左括号
                while(PRI_TOKEN_MAP[opStack.peek] !== PRI_LEFT){
                    calcToken();
                }
                opStack.pop(); // 将左括号弹出，不放在数字栈里
            } else {
                // 将当前符号元素入栈
                opStack.push(token);
            }   
        } else { // 不是操作符就直接拼接在字符串上
            str += token;
        }
    }
    
    // 将符号栈中剩余的元素依次弹出
    while(opStack.peek){
        calcToken();
    }
    return str;
}

console.log(infixToPostfix('1+2*3+4')); // "123*+4+"
console.log(infixToPostfix('1 + 2 *  (4 + 5 - 6) ')); // "1 2 4 5 + 6 - * +"
console.log(infixToPostfix('1 + 2 * (3 + (4 + 5 - 6) * 2)')); // "1 2 3 4 5 + 6 - 2 * + * +"
console.log(infixToPostfix('a + b * c + ( d * e + f ) * g')); // "a b c * + d e * f  + g * +"

前端学数据结构 - 栈（Stack）和队列（Queue）