A. 参考文档

1、教程类

• Heap ：数据结构专辑仓库，有代码有实现，言简意赅；
• 堆和树有什么区别？堆为什么要叫堆，不叫树呢？：知乎问答
• 纸上谈兵: 堆 (heap)：用实际的例子来帮助你理解；
• Binary Heap：geeksforgeeks 有关二叉堆的入门文章
• 二叉堆（Binary Heap）：较为严谨的文章，也有不少的图示；
• 堆的javascript实现：言简意赅，使用 js 实现，具有较高参考价值；
• Implementing a Complete Binary Heap in JavaScript: The Priority Queue：手把手教你实现完全二叉堆
• 数据结构-堆（heap）：主要是介绍了“上滤” 和 “下滤” 的概念
• 最小堆 构建、插入、删除的过程图解：用图详细讲解最小堆的建立和删除操作过程

2、应用

• Heap Data Structure：来自 geeksforgeeks，有关 heap 的 awesome 列表，罗列了有关堆 相关的原理和相关算法题；并有试题 可供测试，看看你能得几分；
• 常用数据结构与算法：二叉堆(binary heap)：从二叉堆的概念到实现，然后还有实例;
• Searching：具体的二叉堆在搜索中的应用；
• HeapSort：geeksforgeeks文章，文字 + 视频讲解堆排序的实现，很直观；

B. 正文

1、下标关系式

堆都能用树来表示，并且一般树的实现都是利用链表。
而二叉堆是一种特殊的堆，它用完全二叉树表示，却可以利用数组实现。

也就说堆并不一定是完全二叉树。平时使用最多的是二叉堆，它可以用完全二叉树表示，二叉堆易于存储，并且便于索引

在堆的实现时，需要注意：

• 因为是数组，所以父子节点的关系就不需要特殊的结构去维护了，索引之间通过计算就可以得到，省掉了很多麻烦。如果是链表结构，就会复杂很多；
• 完全二叉树要求叶子节点从左往右填满，才能开始填充下一层，这就保证了不需要对数组整体进行大片的移动。这也是随机存储结构（数组）的短板：删除一个元素之后，整体往前移是比较费时的。这个特性也导致堆在删除元素的时候，要把最后一个叶子节点补充到树根节点的缘由

二叉堆想树的样子我可以理解，但为什么将它们安排在数组里的话，通过当前下标就能找到父节点和子节点的下标呢？

对于第 i 个节点，即 arr[i]：

• 父节点位置是：arr[(i-1)/2]
• 左子节点：arr[2*i + 1]
• 右子节点：arr[2*i + 2]

为了辅助理解，我们来画个图。按照二叉堆的定义，每个节点下只有 2 个子节点，根据这个特性我们绘制出 N 层情况下这个二叉堆的样子：

• 为方便理解，节点里的数存储的就是数组的下标，从 0 开始按顺序递增
• 通过示意图就能一眼看出下标之间的关系

然后我们将其扁平化放在数组里：

恰好无缝变成一个数组，就成下面那个样子，真的很奇特。

也可以参考文章 Binary Heap

2、下标关系式推导

逆向思维一下，为什么非得用这个数组来表示二叉堆？为什么恰好根节点安排在数组的第 0 个位置，安排在其他的位置可不可以？

好，那我们假设根节点从 5 开始的话，那么问题就变成了，序号下标为 i 的元素，其子元素的下标分别是多少？

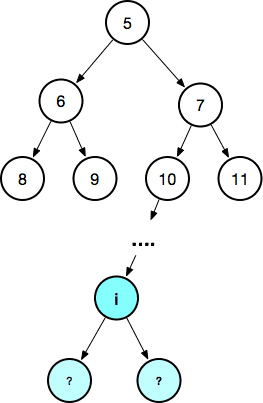
很明显这个数学系采用归纳法就能获得结论。先画出这种情况下的二叉堆图示，相比之前的图加了额外的标注：

从图中可以观察获得基本信息：

• 首先我们设根节点的索引值是 BASE（此例子中， BASE = 5）
• 因为每个节点有 2 个子节点，所以下一层节点个数是当前层个数的 2 倍
• 层数也从 0 开始标识，计算每层的个数：
  • 第 0 层就是根节点，该层共有 1 个节点；
  • 第 1 层有 2 个节点
  • ....
  • 第 n 层就有 2^n 个节点；
• 计算当前层数 之前 累计节点的个数：
  • 第 0 层（根节点），该层之前累计 0 个节点
  • 第 1 层之前累积 1 个节点
  • 第 2 层之前累积 3 个节点
  • ...
  • 第 n 层之前累积 2^n - 1 个节点

然后我们来推导：对于第 n 层中下标为 i 的节点，其对应的子节点的下标的值；

首先令 i 节点在第 n 层的第 k 个位置，将上图中只抽取第 n 层的节点情况，我们这里只关注个数的情况：

• 下标为 i 的节点在第 n 层的第 k 个位置；
• 该节点之前存在 k - 1 个节点
• 该节点之后存在 2^n - 1 个节点

加上之前的结论，我们能用 k、n、BASE 推导出来下标 i 的表达式：

即（后面称之为 下标公式）：

i = 2^n + (BASE-2) + k

如果看得比较晕的话，我们以 BASE = 5 为例，获得第 2 (=n) 层节点、第 3(=k) 个点的情况如下：

其下标：

i = 2^n + (BASE-2) + k = 10

我们看 i 节点的右子节点的表达式是怎么样的。

假设其右节点的下标值为 j，那么不难获得，j 节点是在第 n+1 层的第 2k 的位置，用图说话：

将 n+1、2k 带入到下标公式，就能获得 j 的表达式为：

j = 2^(n+1) + (BASE-2) + 2k

好了，我们就能获得 j 和 i 之间的关系：

j = 2i + (2 - BASE)

所以说，无论 BASE 设置成多少都可以用数组来表示出来，父子节点下标关系都有固定表达式；

既然如此，为何不把 BASE 设置成 0 呢？这样就可以数组下标 0 开始填充数据，而且 不浪费数组空间 了。令 BASE = 0，就能获得熟悉的下标关系表达式；对于第 i 个节点，即 arr[i]：

• 左子节点：arr[2*i + 1]
• 右子节点：arr[2*i + 2]

3、堆的操作

来自文章 纸上谈兵: 堆 (heap)

在 visualgo 网站上有非常好的 可视化操作演示，强烈推荐

堆和队列比较相似，有两个固定的操作：插入和删除。

3.1、插入

在插入操作的时候，会破坏上述堆的性质，所以需要进行名为 上滤（percolate up） 的操作，以进行恢复：

1. 将新元素增加到堆的末尾；
2. 按照优先顺序，将新元素与其父节点比较，如果新元素小于父节点则将两者交换位置；
3. 不断进行第2步操作，直到不需要交换新元素和父节点，或者达到堆顶；
4. 最后通过得到一个最小堆。

这样得到的树，就恢复了堆的性质。我们插入节点 2 为例：

3.2、删除

堆的删除操作与插入操作相反，插入操作从下往上调整堆，而删除操作则从上往下调整堆，该调整的方法称为 下滤（percolate down）：

1. 删除堆顶元素
2. 让最后一个 last 节点成为新的节点，从而构成一个新的二叉树
3. 将 last 节点和两个子节点比较，将小的元素上调。
4. 不断进行步骤，直到 last 节点不大于任一子节点，或者 last 节点成为叶节点

4、堆的应用

4.1、二项堆（Binomial Heap）

• 二项堆(一)之 图文解析 和 C语言的实现：本文会先对二项堆的理论知识进行简单介绍，然后给出C语言的实现。后续再分别给出C++和Java版本的实现；有着非常详细的图解过程；
• Binomial Heap：geeksforgeeks 教程文章
• Binomial heaps & Fibonacci Heaps：很不错的 PPT ，总结了两种堆的具体操作细节；

二项堆是可合并堆，它的合并操作的复杂度是O(log n)。

4.2、斐波那契堆（Fibonacci Heap）

• 斐波那契堆(一)之 图文解析 和 C语言的实现：本文会先对斐波那契堆的理论知识进行简单介绍，然后给出C语言的实现；斐波那契堆比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O(1)
• Fibonacci Heap | Set 1 (Introduction)
• 算法导论笔记：19斐波那契堆：总结了这种堆的性质和用途
• 斐波那契堆（Fibonacci Heap）：较为严谨刻板的教程；
• Fibonacci Heaps：来自普林斯顿大学的 PPT 中大量图示展示具体的堆操作，附带 课程PPT，更多的资料参考 普林斯顿大学官网搜索

斐波那契堆对于 SEARCH 操作的支持比较低效，所以，设计给定元素的操作均需要一个指针指向这个元素

4.3、配对堆（Pairing Heaps）

• 配对堆：阅读成本较低的科普文章，推荐

4.4、左偏树/堆（Leftist Heap）

• Leftist Tree / Leftist Heap：geeksforgeeks 文章
• 纸上谈兵: 左倾堆 (leftist heap)：通俗易懂，推荐阅读；
• 【数据结构与算法】左偏树（堆）的实现：左式堆由于使用二叉链表的存储结构，对动态操作支持良好，在需要合并操作的场合，是极佳的选择。