在总结 栈（Stack） 这个数据结构时候，栈有一种应用是计算算术表达式的 —— 中缀转后缀的。个人对这个算法很感兴趣，就特意找了一下相关的文章，发现中缀表达式转成后缀表达式的算法，有一个专门的名称，叫做 调度场算法（Shunting Yard Algorithm）。

网上大多是讲解具体的编程实现，都缺乏探讨这个算法的实现思想，自己看得非常的迷糊，所以就花费一些时间从自己实现该算法的角度去摸索并且理解这个算法。

A. 参考

1、中缀转后缀

计算器的核心算法-JavaScript实现（逆波兰表达式）：很详细的教程，利用两个栈实现计算器，还有 demo；
javascript使用栈结构将中缀表达式转换为后缀表达式并计算值：例子详实，推荐
How to implement a basic mathematical expression calculator in JavaScript with MathCalc：可以参考现有的 MathCalc 写法
Parse With The Shunting Yard Algorithm Using JavaScript：简略地讲述如何将中缀表达式转换成 RPN，博主的另一篇文章 Evaluate A Reverse Polish Notation Equation With JavaScript 讲解如何基于后缀表达式获取运算结果的
中缀表达式及后缀表达式图解：很详细的图文讲解，每一步都有图示，对初学者很友好；
Codewars：从逆波兰表达式到Three-Pass编译器（1）：看作者是如何举一反三，利用 RPN 完成解题；
如何在程序中将中缀表达式转换为后缀表达式？：知乎问答；

2、调度场算法

在计算机科学里，将中缀形式转换成后缀形式的算法有一个专门的称谓，调度场算法（Shunting Yard Algorithm），看不了的请看下面两篇：

什么是逆波兰表达式？：知乎问答帖，通俗易懂讲解了逆波兰式的优势，不需要两次操作，只要从头扫描到尾就能求出结果，也不需要递归，只需要一个很小的栈就可以。所以逆波兰表达式算法取得了时间复杂度和空间复杂度上的双重优势。有关的历史可以阅读 History of Reverse Polish Notation
调度场算法：文字介绍比较多
调度场算法系列：共 3 篇系列文章，循序渐进剖析调度场算法的来龙去脉，推荐
The Shunting Yard Algorithm：举例理解调度场算法；

3、转换工具类

找了一些在线转换工具，方便快速验证自己实现的转换是否正确

B. 讲解

接下来，我们以 1 + 2 * (3 + (4 + 5 - 6) * 2) 为例讲解；
先用上述中的在线工具，获得中缀表达式对应的后缀表达式是 1 2 3 4 5 + 6 - 2 * + * +

这种后缀表达式对人类理解起来非常的困难，如何让理解的成本低一些呢？

1、回顾小学数学

在小学生级别的算术运算符中，四则运算最为重要的一点是 优先级 —— 优先级高的元素需要先结合运算；优先级高的运算符相当于领导，在计算的时候，也应该贯彻 让领导先走 的理念，优先级高的先结合计算，然后再轮到优先级低的；

四则运算我们粗略分成两类：带括号的 和 不带括号的；

先讨论不带括号的：

式子 1*3+5 肯定是先计算乘法 1*3 (=3) ，然后再计算加法 3+5 (=8)；
式子 1+3*5 肯定是先计算乘法 3*5 (=15)，然后再计算加法 1+15 (=16)

这些道理都懂，很 easy，不过现在让你用栈编程实现，那该如何做？

先不着急实现，我们继续看一下稍微复杂的场景 —— 括号的引入；

让我们重温一下小学数学，当数学老师在黑板上给出 1 + 2 * (3 + (4 + 5 - 6) * 2) 这个式子，我们一眼瞄过去，发现有括号的，优先级提高，所以计算顺序是：

先计算 (4 + 5 - 6) （假设计算结果为 A，值为 3）
然后计算 (3 + A*2)（假设结果为 B，值为 9）
最后计算 1 + 2*B，得到最终结果（假设结果为 C，值为 19）

有 2 个发现：

括号能提升优先级，而且越深的括号优先级越高，越先计算；
最终每一步里，每个括号里面的运算都是 没有括号的基本四则运算

上面讲了一堆的小学数学知识，主要是为了强调运算符的特性，下面会用到。

2、建立两个栈

中缀表达式对人类很友好，不过对计算机运算并非那么友好，我们需要将其转换成计算机语言。

如果从函数的角度来看，四则运算其实可以转换成函数式编程；而我们知道，计算机中就是用栈来实现函数的，所以用栈来实现四则运算是合情合理的选择。

首先，对计算机而言，1 + 2 * (3 + (4 + 5 - 6) * 2) 就是一个字符串，我们挨个读取，然后放到两个栈中：

two stack

左边那个专门存放数字，我们称之为 数字栈 好了；同样的，右边那个专门存放符号，我们称之为 符号栈。

依据第二个结论，括号能提升优先级，而且 括号里面是基础的四则运算，所以我们在上面两个栈中，以括号为 “边界”，划分出子栈来：

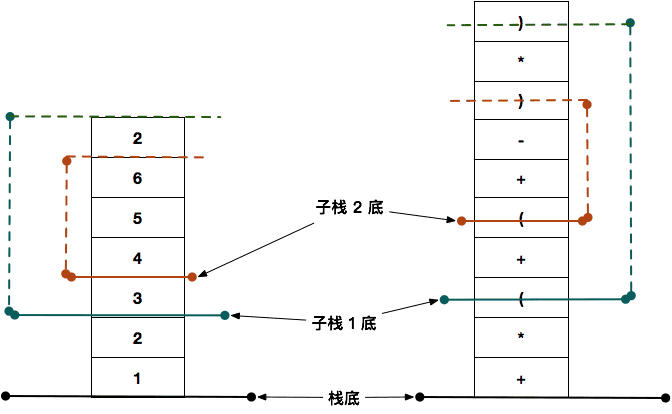
sub stack

有两对括号，所以存在两个子栈；加上整体的栈，可以认为共有 3 个栈
子栈 2 对应最里面的括号，优先级最高；子栈 1 对应次外层的括号，优先级第二高；最外层整体的栈，优先级最低；
每个子栈都对应无括号的四则运算：
- 子栈 2 对应运算 (4 + 5 - 6) （假设计算结果为 A，值为 3），是无括号的四则运算；
- 子栈 1 对应运算 (3 + A*2)（假设结果为 B，值为 9），是无括号的四则运算；
- 基础栈对应 1 + 2*B，得到最终结果（假设结果为 C，值为 19），也是无括号的四则运算

这样对应起来之后，我们就会发现，使用栈和子栈的概念来处理四则运算真的很贴切！

先来看看无括号的四则运算（子栈）实现。

2.1、子栈的计算实现

由于每个子栈都是无符号四则运算（且计算结果是具体的数值），我们看如何借助栈进行简单的、无括号的四则运算，以 1+ 2 * 3 + 4 为例：

依据算术表达式，我们绘制出其数字栈和符号栈：

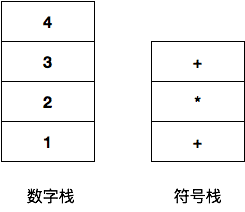
two stack

由于 *（乘法）的优先级比 +（加法）要高，所以肯定要先计算 2*3，那么像上图中符号栈那样把 + 压在 * 是肯定不行的，因为会先弹出 + 号，进行 3 + 4 的运算，那怎么办？

当某个符号准备入栈（符号栈）的时候要进行判断，确保栈中 “压” 在自己下的符号的优先级要比自己低，否则需要将栈顶的元素弹出来执行计算。

为了形象记忆，形象些来记忆，高级领导总不能被压在低层领导下吧，“让领导先走”

上图中符号栈中，当第三个 + 准备入栈的时候，发现栈顶元素是 * 号，优先级比自己高，需要将该 * 先弹出来，和数字栈中的 2 和 3 执行运算：

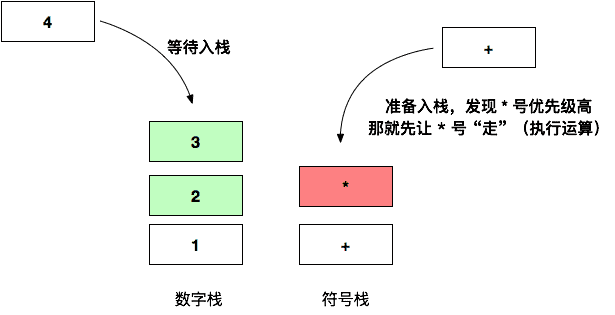
执行乘法运算

然后将计算结果 6 放到数字栈中，执行完后 + 还想继续入栈发，唉，此时发现栈顶是 + 元素，优先级和自己的一样！毕竟有个先来后到，虽然等级一样，毕竟人家资历老，所以优先让它先 “走”（执行运算）：

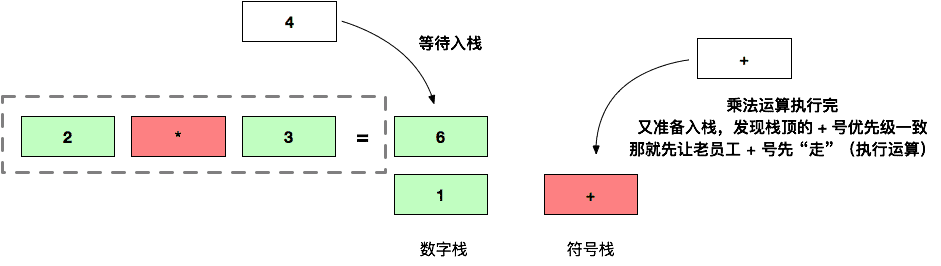
执行加法运算

将计算结果 7 放入到数字栈，此时栈为空，等待良久的 + 符号总算可以入栈了：（同时还有数字 4 压入到数字栈）

加法运算

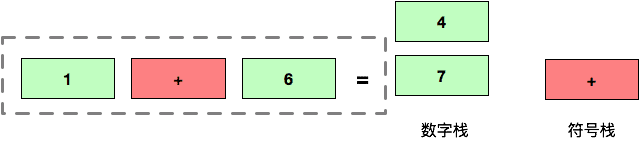
由于此时后续没有符号入栈了，所以挨个弹出符号栈中的运算符，这里只剩下一个 + 号，就将它弹出来然后执行运算，获得最终的计算结果 11。

result

到这一步，两个栈都为空，获得的最终数值 11 就是我们要计算的算式的最终结果了。

2.2、复合栈计算

下面讨论利用栈完成带括号的四则运算，这种用于处理带括号的栈，我们暂且称之为 复合栈（自己创建的概念）

从之前的讨论我们得知，带括号的部分，相当于是子栈，里面所进行的就是刚讨论过的无括号的四则运算；而且每个子栈的运算结果都是具体数值，放在左边的数字栈中去。

所以遇到括号，就相当于进入到 子栈运算环节，括号越深表明优先级越高，越需要先计算；计算完成之后，肯定变成一个数字，之后再进入到其父单元的四则运算逻辑中；以本文讨论的 1 + 2 * (3 + (4 + 5 - 6) * 2) 为例

肯定是先计算子栈 2 所对应的 (4 + 5 - 6)
然后再计算子栈 1 所对应的 (3 + 3 * 2)
最后再计算基础栈 1+ 2 * 9

从这里看出，带括号的四则运算就相当于是子栈运算的递归版本。

计算的思路也很套路：

从左向右挨个读取字符，分别放到数字栈和符号栈中
在符号栈运行的时候，对比符号的优先级，确保 高优先级的符号 压在 低优先级符号上；如果不是，则需要弹出高优先级符号，进行即时运算，将运算结果放在左边的数字栈中；
遇到左括号表明进入子栈，遇到右括号表示该子栈完结，需要将子栈里残余的符号都清空，将该子栈中运算执行完变成 子计算结果值 放到数字栈中；
按照这样的规则一直读完表达式字符；
将剩下的字符栈挨个弹出来执行计算，获取最终的结果。

注：需要注意括号的优先级，括号的优先级最高，但由于它表示的 子栈的分隔符（左括号表示子栈的开始，右括号表示子栈的结束），所以不参与符号优先级的对比

我们分步图示 1 + 2 * (3 + (4 + 5 - 6) * 2) 这个示例中，刚开始我们从左到右读取字符，分别将数字和符合压入栈，直到遇到准备压入 5 - 6 中的 - 符号时，发现栈顶是同级别的加号 +，需要弹出加号做加法运算 4 + 5：

弹出加号

这里要注意，在压入符号栈的过程中，如果遇到左括号先不用管，也先压入符号栈，左括号的优先级虽然比 + 高，但仍旧被压在 + 下；这么操作的原因是左括号 它表示的子栈的开始，起分隔子栈的作用，而不参与优先级的比对逻辑；

四则运算中的括号相当于函数中的 作用域 ；

继续我们的压栈操作直到遇到 第一个右括号，表明是一个子栈结束，依次弹出符号栈中元素做运算直到遇到左括号为止：

minus

这个过程相当于执行 (9 - 6) 操作，操作至此我们就消灭了 子栈 2，整体消灭的过程相当于执行 4 + 5 - 6 无括号的四则运算，然后获得的计算结果 3 放到左边的数字栈；

继续将读取算术表达式的字符放入数字栈和符号栈，直到最后一个右括号，表明又要结束一个子栈（子栈 1 ）了；依次弹出符号栈中元素做运算，直到遇到左括号为止：

stack1

这个过程相当于执行 3 + 3 * 2 无括号四则运算操作，将计算的结果 9 放入到左边的数字栈：

stack0

此时子栈都已经 “消灭” 完了，剩下最外层的基础栈，肯定无括号，按照无括号四则运算操作分分钟获得最终结果 19。

最好自己绘制一下这些栈体验上述的流程，这样就能理解栈在其中所起到关键作用；

在上述运算的过程，是数字栈和符号栈 “生长 - 消亡” 的过程，借助这个过程中我们可以获得一些 “中间产物”；

2.3、获取 AST

首先就是获得抽象语法树（AST，Abstract Syntax Tree）。

如果让你完成一项解析器，你首先是要对中缀表达式 1 + 2 * (3 + (4 + 5 - 6) * 2) 进行语法解析，整理成 抽象语法树，会成下面那样子：

ast

在上述复合栈运算的过程中，我们是可以获得上述的语法树。

这里需要用到二叉树这种数据结构，在每个运算的步骤中我们稍作改动 —— 我们将入栈的数字改成二叉树就行了，其他地方不变。

比如计算完 4 + 5 的时候是这样的：

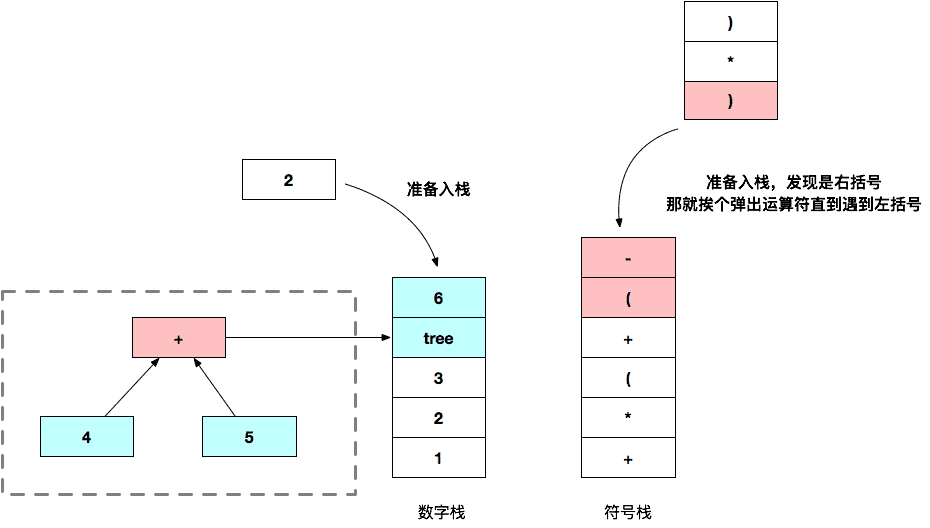
tree1

计算完 4 + 5 - 6 的时候如下：

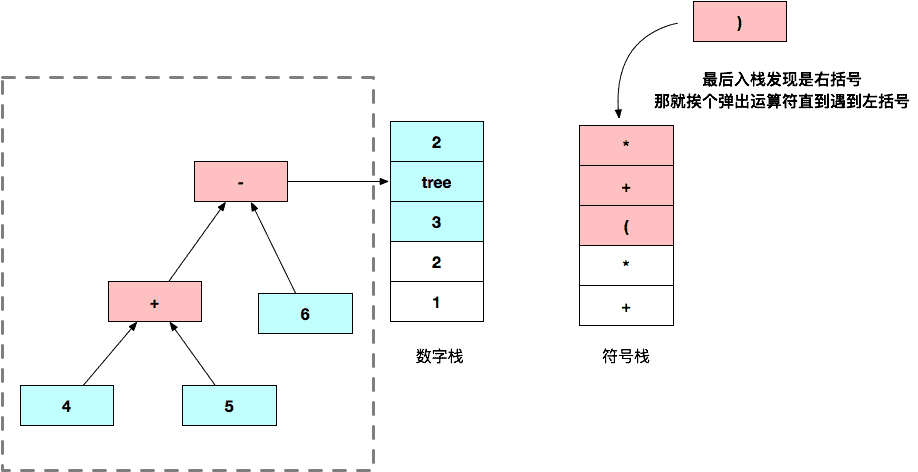
tree2

...

一直下去直到两个栈都为空，就获得了完整的一颗抽象语法树。

稍微总结一下：

生成子树的时候，以符号为父节点，取出两个数字堆栈的成员为子节点；
生成的树压回到数字堆栈中；
运算过程，是自底向上产生AST的，即先获得最深部分的子树，然后往上构建从而获得整棵树；
计算优先级越高的部分，在语法树的位置越深

3、调度场算法

上面全是铺垫，现在要讲的才是重点。

我们上述是采用两个栈完成算术运算，能否合并采用一个栈呢？

答案是可以的，如何合并呢？直接把符号栈堆放到数字栈上呢？或者，把数字栈放到符号栈上？no no no，是不行的，太简单粗暴了。

combine

那怎么合成？

3.1、看成一个整体

还是要从复合栈的运算中找思路。

仍旧以 1+ 2 * 3 + 4 简单的无括号算术运算为例，我们对比一下如何符号不运算，而是直接放入到符号栈会是怎样的：

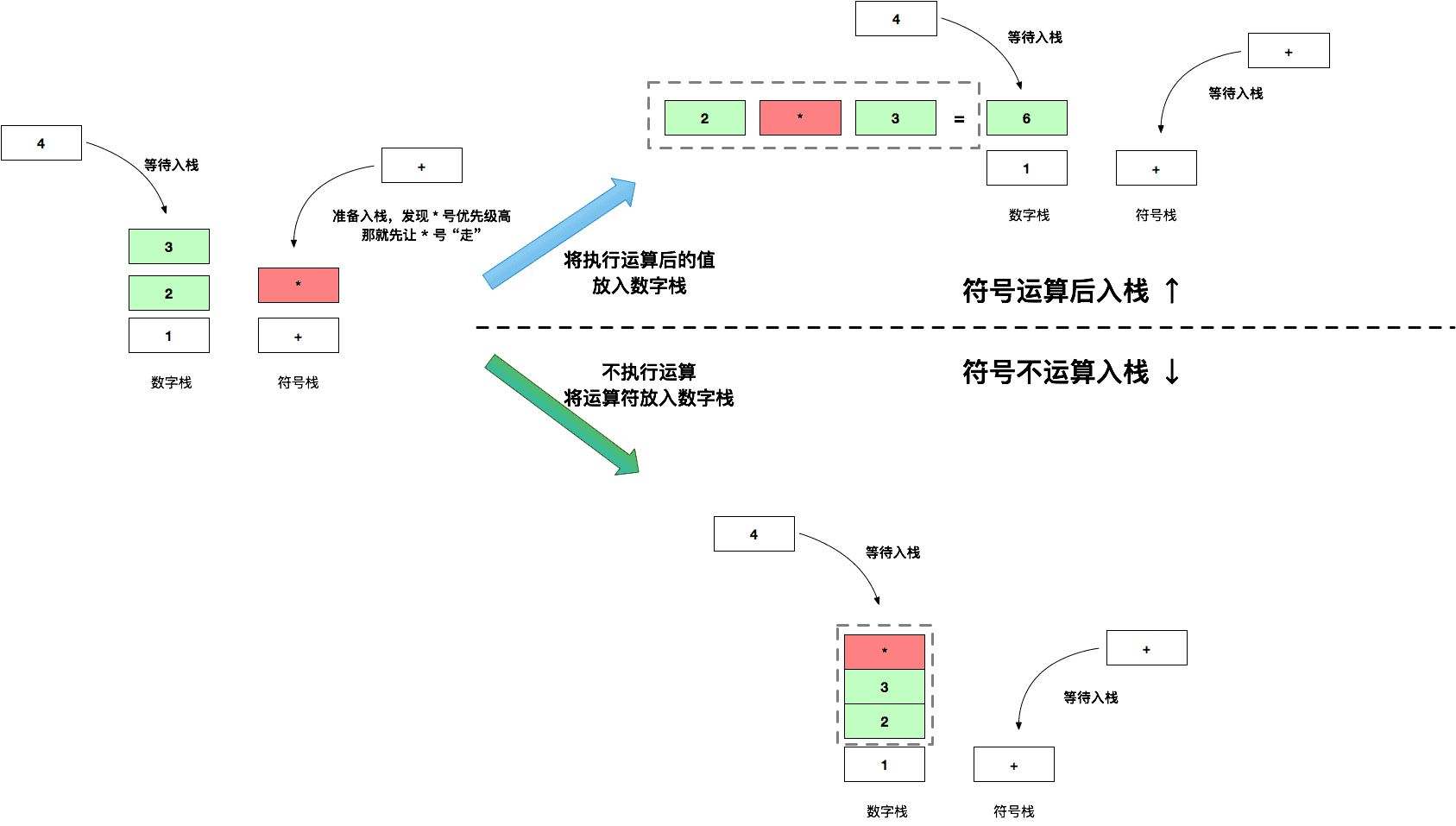
compare

图片右上部分是原来的逻辑，将 + 和左边的运算符运算之后放入到数字栈中，而右下角则不进行运算，直接将符号放到数字栈中。想象一下，运算结果值 6 其实就是右下角的 23+ 子栈，后续的运算我们都把 23+看成一个整体（你就想象成数字 6）就可以了。

继续下一步的运算 1 + 6 （这里的 6 就是 23+ 这个子栈整体）后，两种运算方式栈的情况如下：

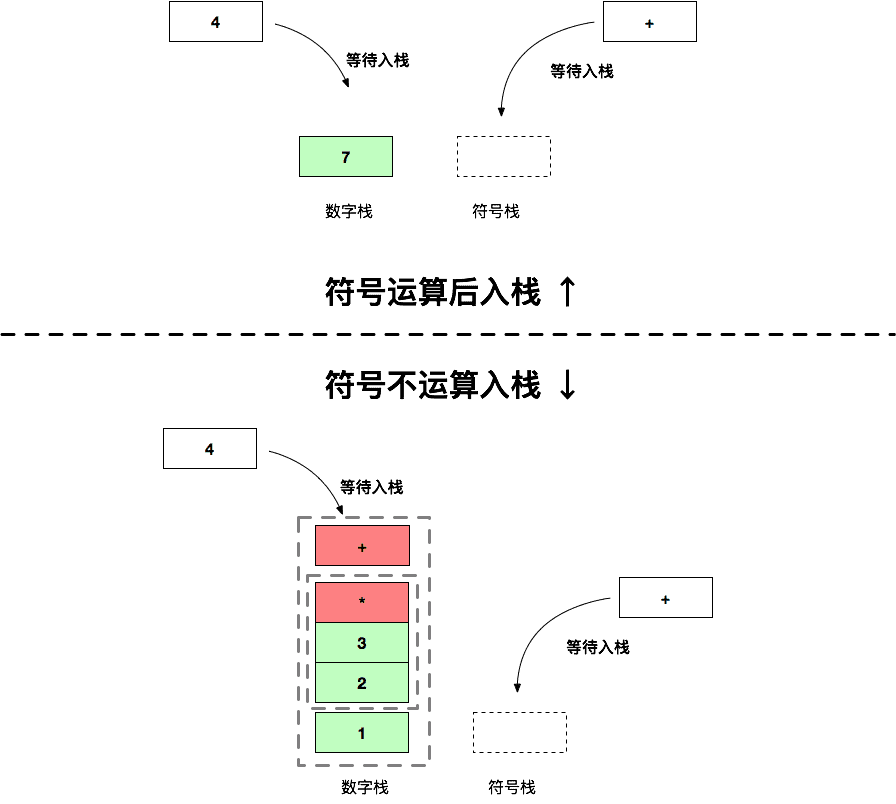
step 2

我们发现直接运算后的栈会清爽很多；而符号不参与不运算时，相当于是把右边的符号栈挪到了数字栈，所以看上去左边的栈 “臃肿” 了许多，这是因为节省了运算的步骤。

继续最后一步 7 + 4，两种运算方式栈的情况如下：

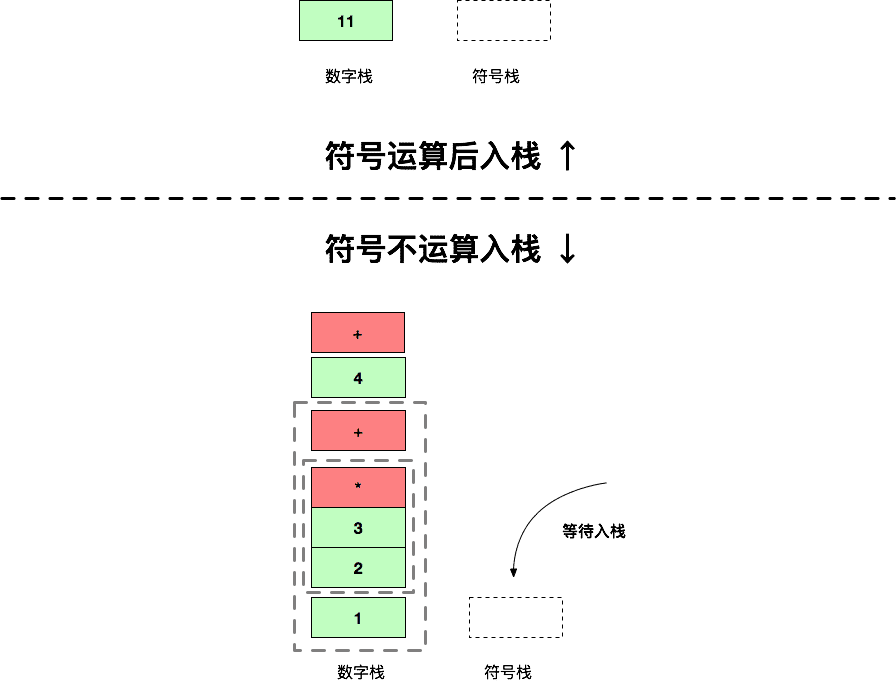
step3

到这一步你会发现，上面那种符号直接运算的情况，就能获得最终运算结果 11；而下面那种符号不直接运算的情况，则是获得混合数字和符号的栈，获得这个栈的操作过程就是著名的 调度场算法，而从栈底部往上的字符串 123*+4+ 就是 逆波兰表达式。

由于调度场算法的时候，左边的数字栈只有压栈操作并没有弹栈操作，所以可以用字符串、数组或者队列来代替，这样就只剩下右边的符号栈了，所以可以只用一个栈实现 调度场算法。

获得的逆波兰表达式并非最终的运算结果的，如果需要获得最终结果还需要一次逆向弹栈的操作。因此：

如果你仅仅是需要获取运算的最终结果，推荐使用符号运算后入栈的方式
如果想要获得逆波兰表达式，就不得不使用调度场算法；

上面我们讨论无括号的简单四则运算场景下调度场的算法步骤，加入括号之后，我们可以依样画葫芦获得其算法步骤 —— 正如之前我们如何依据子栈结果获得复合栈的运算结果那样。限于篇幅，这儿就不继续展开。

3.2、程序代码实现

按照上面的思路，这里我们仅仅列举出将中缀转换过程后缀表达式的函数：

/* ----------------------------------------------------
    调度场算法，将中缀转换过程后缀表达式
----------------------------------------------------- */
var Stack = require("ss-stack");

// 操作符优先级列表
var PRI_LEFT = 99;
var PRI_RIGHT = 100;
var PRI_TOKEN_MAP = {
    '+': 1,
    '-': 1,
    '*': 2,
    '/': 2,
    '(': PRI_LEFT,
    ')': PRI_RIGHT,
};

// 将中序转换成
function infixToPostfix(expression){
    expression = expression.replace(/\s*/g,""); // 去除所有空白字符
    var opStack = new Stack();
    var str = '';
    
    
    // 符号栈操作
    function calcToken(){
        str += opStack.pop();
    }
    
    for(let token of expression){
        var tokenPri = PRI_TOKEN_MAP[token] || 0;
        var peekTokenPri = opStack.peek && PRI_TOKEN_MAP[opStack.peek] || 0;   
        
        
        // console.log(opStack.stack.toArray());
        // 首先判断是否操作符
        if(tokenPri){
        
            // 情况 1： 栈顶不是左括号；入栈符号不是右括号
            // 循环判断当前栈顶符号，且优先级高于或等于将要入栈的元素，且栈顶不是左括号
            while(opStack.peek && PRI_TOKEN_MAP[opStack.peek] !== PRI_LEFT && tokenPri !== PRI_RIGHT && peekTokenPri >= tokenPri) {
                calcToken();
            }
            
            // 情况2：右括号准备入栈，
            if(tokenPri === PRI_RIGHT){
                // 将符号栈中元素依次弹出，则需要弹栈一直到左括号
                while(PRI_TOKEN_MAP[opStack.peek] !== PRI_LEFT){
                    calcToken();
                }
                opStack.pop(); // 将左括号弹出，不放在数字栈里
            } else {
                // 将当前符号元素入栈
                opStack.push(token);
            }   
        } else { // 不是操作符就直接拼接在字符串上
            str += token;
        }
    }
    
    // 将符号栈中剩余的元素依次弹出
    while(opStack.peek){
        calcToken();
    }
    return str;
}

console.log(infixToPostfix('1+2*3+4')); // "123*+4+"
console.log(infixToPostfix('1 + 2 *  (4 + 5 - 6) ')); // "1 2 4 5 + 6 - * +"
console.log(infixToPostfix('1 + 2 * (3 + (4 + 5 - 6) * 2)')); // "1 2 3 4 5 + 6 - 2 * + * +"
console.log(infixToPostfix('a + b * c + ( d * e + f ) * g')); // "a b c * + d e * f  + g * +"

代码的运行结果代码放在 https://runkit.com/boycgit/ss-stack 这儿了，此外还给出了直接计算出结果的函数，和上述的过程几乎一样，不一样的地方在于 calcToken 的内容，一个是不做计算进行字符拼接，另一个则是做了计算直接放入到数字栈中；

注意：函数实现的时候注意边界条件，尤其是 括号符号的处理。

4、练习

自己手动使用调度栈将 a + b * c + ( d * e + f ) * g 转换成后缀表达式。
答案： a b c * + d e * f + g * +

5、总结

在本篇文章中，为了理解调度场算法，我们首先使用两个栈（数字栈和符号栈）来分析运算的过程，从简单的四则运算开始到复杂的带括号的四则运算。

先分析简单的四则运算，这样能减轻理解上的难度，比较直观地展示栈在算术运算中所发挥的作用；随后我们逐步推演，将两个栈归并到单个栈运算，就完成了调度场算法。在推演的过程中，还自底向上获得了 AST 。

调度场算法的核心就在于用栈暂存符号以备“调度”，比较新符号和栈顶原有的符号，选择其中更容易结合的（根据优先级、结合方向）出栈——更容易结合就意味着更早地参与计算。理解这点以后，调度场算法就仿佛显而易见、理所当然地存在了。

如果你学过树（Tree）数据结构和算法，你会发现调度场算法其本质就是上述 AST 二叉树的深度优先遍历算法中的 后续遍历算法；这么盘算下来，哟，殊途同归啊，很奇妙的感觉。如果你不好理解调度场算法的话，可以先列出算式对应的 AST，然后在做一把后续遍历就能获得逆波兰式；

本文完。

算法 - 调度场算法（Shunting Yard Algorithm）